ত্রিকোণমিতিক পরিচয়ের ধারণা হল একটি ধারণা যা গণিতের ক্ষেত্রে ব্যবহার করা হয় পরিবর্তনশীল ত্রিকোণমিতিক ফাংশনগুলি বোঝাতে যা একটি জ্যামিতিক চিত্রে পাওয়া যায়। ত্রিকোণমিতি হল গণিতের একটি শাখা যা ত্রিভুজগুলির বিশ্লেষণ এবং অধ্যয়নে বিশেষ করে, বিশেষ করে বিদ্যমান বিভিন্ন কোণের আকার, অর্থ এবং মানগুলিতে। ত্রিকোণমিতিক পরিচয়গুলি তখন সেই মানগুলির ফলাফল হবে যা পরিবর্তনশীল এবং একটি থেকে অন্যটির মধ্যে খুব বৈচিত্র্যময়।
গণিতের অনেক উপাদানের মতো, ধারণাগুলি প্রাচীনকাল থেকেই বিদ্যমান ছিল যেখানে গ্রীক দার্শনিকরা ইতিমধ্যে জ্যামিতিক পরিসংখ্যানগুলির কোণের কার্যাবলী এবং মানগুলির ধারণাগুলি প্রতিষ্ঠা করেছিলেন। এই ধারণাগুলি কেবলমাত্র আধুনিকতায় উন্নত হবে, সপ্তদশ শতাব্দীতে যখন তারা বিভিন্ন কোণগুলির মধ্যে সমস্ত ধরণের গণনা করতে সক্ষম হওয়ার জন্য বীজগণিতিকভাবে উল্লেখ করা হয়েছিল।
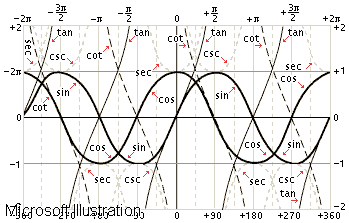
ত্রিকোণমিতিক পরিচয়গুলিকে বিস্তৃতভাবে সমস্ত সম্ভাব্য কোণ ভেরিয়েবল হিসাবে সংজ্ঞায়িত করা যেতে পারে যা একটি জ্যামিতিক চিত্রে থাকতে পারে। এই পরিচয়গুলি সর্বদা গ্রীক অক্ষর যেমন আলফা, বিটা, ওমেগা ইত্যাদি থেকে উপস্থাপন করা হয়। ডিগ্রী সেন্টিগ্রেডের মতো উপাদানগুলিও প্রতিটি পরিচয়ের ভেরিয়েবল স্থাপন করতে ব্যবহৃত হয়। সাইন এবং কোসাইন, সাইন এবং ট্যানজেন্ট ইত্যাদির মধ্যে যেগুলি প্রতিষ্ঠিত হয় সেগুলি সবচেয়ে বেশি পরিচিত। ত্রিকোণমিতিক পরিচয় হল সরলীকৃত ফর্ম যা আমাদের ত্রিকোণমিতির বিভিন্ন ফাংশন সঞ্চালন এবং জানতে দেয়। গণিতের এই সমস্ত প্রশ্ন, আরও বিশেষভাবে ত্রিকোণমিতির, বিভিন্ন গণনাকে সংগঠিত করতে পরিবেশন করে যা প্রতিটি ধরণের ডেটার নির্দিষ্ট ফাংশন থেকে করা উচিত। ত্রিকোণমিতিক পরিচয়গুলি অত্যন্ত পরিবর্তনশীল এবং প্রতিটি ত্রিকোণমিতিক ফাংশন (অর্থাৎ, মানগুলি) প্রতিটি ক্ষেত্রে অনুসারে বিভিন্ন এবং নির্দিষ্ট উপায়ে উপস্থাপন করার জন্য বিভিন্ন সম্ভাবনার অনুমতি দেয়।
