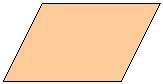
ক্ষেত্রে জ্যামিতি ক রম্বয়েড এটাই একটি সমান্তরাল বৃত্ত (বিশেষ ধরনের চতুর্ভুজ, যার বাহু দুটি দুই দ্বারা সমান্তরাল) যার সন্নিহিত বাহুগুলি অসম এবং এর দুটি কোণ অন্য দুটি থেকে বড়; অর্থাৎ, একটি রম্বয়েড, এটি একটি রম্বস বা আয়তক্ষেত্র নয়.
এটা উল্লেখ করা উচিত যে হীরা এটি একটি সমান্তরাল চতুর্ভুজ যার চারটি বাহুর দৈর্ঘ্য সমান, অন্যদিকে বিপরীত অভ্যন্তরীণ কোণগুলি সমান, কর্ণগুলি একে অপরের সাথে লম্ব এবং তাদের প্রত্যেকটি অন্যটিকে সমান অংশে বিভক্ত করে; এবং আয়তক্ষেত্র একটি সমান্তরালগ্রাম যার চারটি বাহু একে অপরের সমকোণে অবস্থিত। এর পরিধি এর সকল বাহুর সমষ্টির সমান এবং ক্ষেত্রফল এর দুটি সন্নিহিত বাহুর গুণফলের সমান।
সাধারণত এটিকে সরাসরি সমান্তরালগ্রাম বলা হয় বা আমরা এটিকে একটি অ-আয়তাকার সমান্তরাল হিসাবেও খুঁজে পেতে পারি।
রম্বয়েডের সবচেয়ে উল্লেখযোগ্য বৈশিষ্ট্যগুলির মধ্যে আমরা নিম্নলিখিতগুলি খুঁজে পাই: এর দুটি জোড়া সমান বাহু রয়েছে, একে অপরের সমান্তরাল, বিপরীত কোণগুলি সমান, সংলগ্ন কোণগুলি সম্পূরক, অর্থাৎ, দুটির যোগফল আমাদের দেয় 180 ° , যেহেতু এটি একটি রম্বস নয়, যেমনটি আমরা উপরে বলেছি, এর কর্ণগুলি একে অপরের সাথে লম্ব নয় এবং এটি একটি আয়তক্ষেত্রও নয়, এর তির্যকগুলি সমান নয় এবং যদি এর অভ্যন্তরীণ কোণগুলি যোগ করা হয় তবে এটি আমাদের যে চিত্রটি দেয় তা হল 360 °
অন্যদিকে, এর পরিধি 2 এর সমান এবং ক্ষেত্রফল পাওয়া যাবে এক বাহুর দৈর্ঘ্যকে সেই বাহুর ও বিপরীত দিকের মধ্যবর্তী লম্ব দূরত্ব দ্বারা গুণ করার পর, অর্থাৎ উচ্চতা।
