রৈখিক সমীকরণের সংজ্ঞা

যে ধারণাটি আমরা নীচে মোকাবেলা করব তা ক্ষেত্রের সাথে যুক্ত গণিত, এদিকে, এই বিজ্ঞানের জন্য, ক সমীকরণ তাই কি সমতা যাতে অন্তত একটি অজানা উপস্থিত হয়, যেহেতু আরও কিছু থাকতে পারে, যা তার রেজোলিউশনে পৌঁছানোর জন্য প্রকাশ করা আবশ্যক।

এখন, সমীকরণের উপাদান রয়েছে যেমন: সদস্য, যা প্রতিটি বীজগাণিতিক রাশি, যে, পরিচিত মান, এবং অন্যদিকে অজানা, যা অবিকল সেই মানগুলি আবিষ্কার করার জন্য। বিভিন্ন গাণিতিক অপারেশনের মাধ্যমে আমরা অজানা তথ্য জানতে সক্ষম হব।

একটি সমীকরণে বর্ণিত পরিচিত মানগুলি থাকতে পারে সংখ্যা, চলক, ধ্রুবক, বা সহগ, যখন অজানা বা অজানা মানগুলি অক্ষর থেকে প্রতীকী হবে যা পরে জানা যাবে এমন মান হিসাবে কাজ করে।

একটি উদাহরণ দিয়ে আমরা এটি আরও স্পষ্টভাবে দেখতে পাব: 10 + x = 20. এই সহজ সমীকরণে সংখ্যা 10 এবং 20 আমরা জানি মান এবং এক্স আমরা জানি না যে এক এবং খুঁজে বের করতে হবে. রেজোলিউশন এই মত হবে: x = 20 - 10, তাই x = 10। সমীকরণে অজানা 10 হবে.

বিভিন্ন ধরনের সমীকরণ আছে, যার মধ্যে বীজগণিত সমীকরণ উদ্বেগের ধরন অবস্থিত, যা এর প্রথম ডিগ্রি সমীকরণ বা রৈখিক সমীকরণ. এটি এমন এক ধরনের সমীকরণ যা শুধুমাত্র প্রথম পাওয়ারের সাথে একটি চলকের যোগ এবং বিয়োগকে জড়িত করবে।

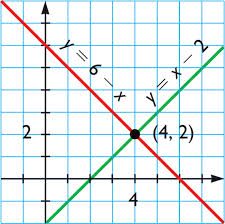
এই ধরনের সমীকরণের সহজতম ফর্মগুলির মধ্যে একটি হল: y = mx + n (কার্টেসিয়ান সিস্টেমে তারা রেখা দ্বারা প্রতিনিধিত্ব করা হয়), তারপর m হবে ঢাল এবং n যে বিন্দুতে রেখাটি y-অক্ষকে ছেদ করে… 4 x + 3 y = 7।